Geometry Processing and Visualization

Import

import igl
import meshplot as mp
import numpy as np

Geometry Representation

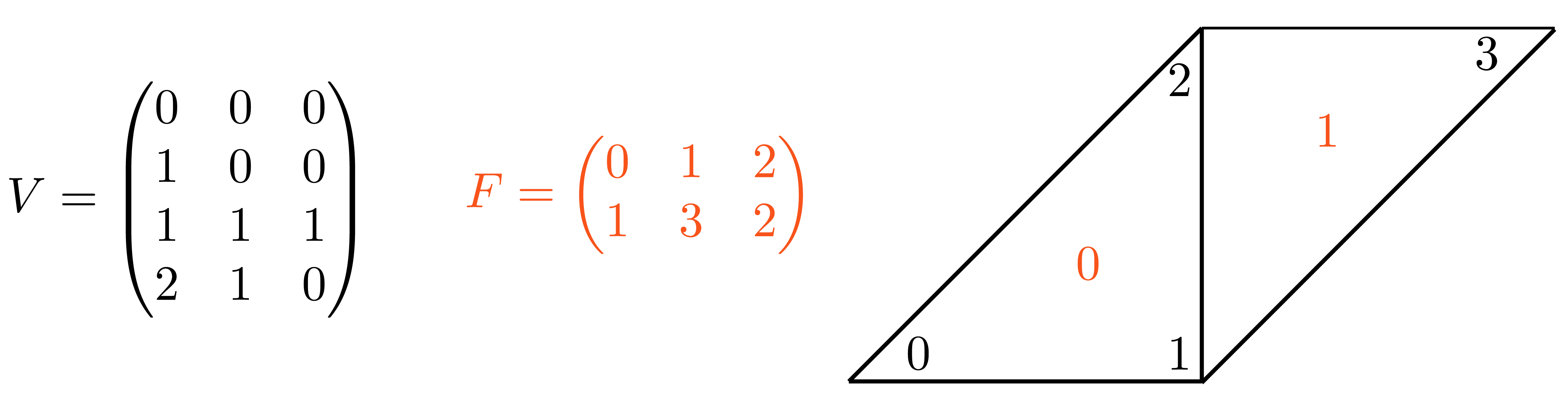
v = np.array([
    [0., 0, 0],
    [1, 0, 0],
    [1, 1, 1],
    [2, 1, 0]])

f = np.array([
    [0, 1, 2],
    [1, 3, 2]])

mp.plot(v, f)

Geometry Loading and Saving

# Read bunny and retrieve shape
v, f = igl.read_triangle_mesh("data/bunny.obj")
print(v.shape, f.shape)

# Write bunny
igl.write_triangle_mesh("data/bunny_new.off", v, f)

# Visualize bunny
mp.plot(v, f)

(3485, 3) (6966, 3)

Visualizing Surfaces and Pointclouds

# Visualize surface mesh and point cloud (with colors)
mp.plot(v, f, c=v[:, 0])

mp.plot(v, c=v[:, 0])

Scalar and Vector Field Visualization - Normals

nf = igl.per_face_normals(v, f, np.zeros(3))
mp.plot(v, f, c=np.abs(nf), shading={"roughness": 1.0})

nv = igl.per_vertex_normals(v, f)

p = mp.plot(v, c=np.abs(nv))
p.add_lines(v, v + nv * 5e-3)

Scalar and Vector Field Visualization - Curvature

# Calculate principal curvature
d1, d2, k1, k2 = igl.principal_curvature(v, f)

# Calculate mean curvature for color coding
mean_curv = 0.5 * (k1 + k2)

p = mp.plot(v, f, c=mean_curv)

p.add_lines(v + d1 * 2e-3, v - d1 * 2e-3, shading={"line_color": "red"})
p.add_lines(v + d2 * 2e-3, v - d2 * 2e-3, shading={"line_color": "yellow"})

Saving Results and Offline Visualization

# Save the previous result
p.save("test1.html")

Plot saved to file test1.html.

Saving Results and Offline Visualization

# Load a new mesh
v1, f1 = igl.read_triangle_mesh("data/bumpy.off")

# Switch to offline plotting
mp.offline()
mp.plot(v1, f1, c=np.random.rand(*f1.shape), filename="test2.html")

Plot saved to file test2.html.

# Switch to jupyter plotting
mp.jupyter()
p = mp.plot(v1, f1, c=np.random.rand(*f1.shape))
p.add_mesh(v1 + 5, f1, c=v1[:,1])
p.add_points(v1 - 5, c=v1[:,2], shading={"point_size": 1.0})
p.save("test3.html")

Plot saved to file test3.html.

Mesh Statistics

v, f = igl.read_triangle_mesh("data/bunny.obj")

# Irregular vertices, the border is ignored
irregular = igl.is_irregular_vertex(v, f) 
irregular_ratio = np.sum(irregular) / v.shape[0]
print("Irregular vertices:\n%d/%d (%.2f%%)\n"%
      (np.sum(irregular), v.shape[0], irregular_ratio * 100))

# Compute areas, min, max and std
area = igl.doublearea(v, f) / 2.0
area_avg = np.mean(area)
area_min = np.min(area) / area_avg
area_max = np.max(area) / area_avg
area_ns = (area - area_avg) / area_avg
area_sigma = np.sqrt(np.mean(np.square(area_ns)))
print("Areas Min/Max/Sigma: \n%.2f/%.2f/%.2f\n"%
      (area_min, area_max, area_sigma))

# Compute per face angles, min, max and std
angles = igl.internal_angles(v, f)
angles = 360.0 * (angles / (2 * np.pi))
angle_avg = np.mean(angles)
angle_min = np.min(angles)
angle_max = np.max(angles)
angle_ns = angles - angle_avg
angle_sigma = np.sqrt(np.mean(np.square(angle_ns)))

print("Angles in degrees Min/Max/Avg/Sigma: \n%.2f/%.2f/%.2f/%.2f\n"%
      (angle_min, angle_max, angle_avg, angle_sigma))

Irregular vertices:
2139/3485 (61.38%)

Areas Min/Max/Sigma: 
0.04/11.24/0.57

Angles in degrees Min/Max/Avg/Sigma: 
2.74/172.13/60.00/25.14

Geometry Processing and Visualization - Advanced

Texture Mapping (Harmonic Parametrization)

vc, fc = igl.read_triangle_mesh("data/camelhead.off")
p3d = mp.plot(vc, fc)

# Compute and visualize boundary vertices
bnd = igl.boundary_loop(fc)
p3d.add_points(vc[bnd], shading={"point_size": 0.1})

# Map boundary vertices to circle
bnd_uv = igl.map_vertices_to_circle(vc, bnd)

# Calculate harmonic weight functions and plot the mesh
uv = igl.harmonic_weights(vc, fc, bnd, bnd_uv, 1)
mp.plot(uv, fc, uv=uv, shading={"wireframe": True, "wire_color": "red"})

# Plot with mapped texture
mp.plot(vc, fc, uv=uv)

Texture Mapping (Least Square Conformal Maps)

# Fix two points on the boundary
b = np.array([2, 1])
b[0] = bnd[0]
b[1] = bnd[int(bnd.size / 2)]

bc = np.array([[0.0, 0.0], [1.0, 0.0]])

# LSCM parametrization
_, uv_l = igl.lscm(vc, fc, b, bc)

mp.plot(vc, fc, uv=uv_l)

mp.plot(uv_l, fc, uv=uv_l, shading={"wireframe": True, "wire_color": "red"})

Texture Mapping (As-Rigid-As-Possible)

# Fix vertex 0 and use harmonic uv as initial guess
arap = igl.ARAP(vc, fc, 2, np.zeros(0))
uv_a = arap.solve(np.zeros((0, 0)), uv)

mp.plot(vc, fc, uv=uv_a)

mp.plot(uv_a, fc, uv=uv_a, shading={"wireframe": True, "wire_color": "red"})

Shape Filtering (Laplacian Smoothing)

from scipy.sparse.linalg import spsolve

v, f = igl.read_triangle_mesh("data/cow.off")

l = igl.cotmatrix(v, f)
vs = [v]
for i in range(10):
    m = igl.massmatrix(v,f,igl.MASSMATRIX_TYPE_BARYCENTRIC)
    v = spsolve(m - 0.001 * l, m.dot(v))
    vs.append(v)

mp.plot(vs[0], f)

mp.plot(vs[5], f)

mp.plot(vs[9], f)

Shape Filtering (Spectral Smoothing)

from scipy.sparse.linalg import eigsh

v, f, _ = igl.read_off("data/cow.off")
l = igl.cotmatrix(v, f)

d, u = eigsh(-l, 200, which="SM")
vs = u @ u.T @ v

mp.plot((u[:, :10] @ u[:, :10].T) @ v, f)

Shape Deformation (Biharmonic Deformation)

v, f = igl.read_triangle_mesh("data/decimated-max.obj")
v[:,[0, 2]] = v[:,[2, 0]] # Swap X and Z axes

s = igl.read_dmat("data/decimated-max-selection.dmat")
b = np.array([[t[0] for t in [(i, s[i]) for i in 
             range(0, v.shape[0])] if t[1] >= 0]]).T

u_bc = np.zeros((b.shape[0], v.shape[1]))
v_bc = np.zeros((b.shape[0], v.shape[1]))

for bi in range(b.shape[0]):
    v_bc[bi] = v[b[bi]]
    if s[b[bi]] == 0: # Don't move handle 0
        u_bc[bi] = v[b[bi]]
    elif s[b[bi]] == 1: # Move handle 1 down
        u_bc[bi] = v[b[bi]] + np.array([[0, -50, 0]])
    else: # Move other handles forward
        u_bc[bi] = v[b[bi]] + np.array([[-25, 0, 0]])

d_bc = 0.5 * (u_bc - v_bc)
d = igl.harmonic_weights(v, f, b, d_bc, 2)
mp.plot(v+d, f, -s)

Shape Deformation (As-Rigid-As-Possible)

v, f = igl.read_triangle_mesh("data/decimated-knight.off")
s = igl.read_dmat("data/decimated-knight-selection.dmat")

# Vertices in selection
b = np.array([[t[0] for t in [(i, s[i]) for i in 
            range(0, v.shape[0])] if t[1] >= 0]]).T

arap = igl.ARAP(v, f, 3, b)

# Set color based on selection
c = np.ones_like(f) * np.array([1.0, 228/255, 58/255])
for fi in range(0, f.shape[0]):
    if np.all(s[f[fi]] >= np.array([0, 0, 0])):
        c[fi] = np.array([80/255, 64/255, 1.0])

t = 5.0
bc = np.zeros((b.size, v.shape[1]))
for i in range(0, b.size):
    bc[i] = v[b[i]]
    if s[b[i]] == 0:
        bc[i, 0] += t * 0.02 - 0.12
    elif s[b[i]] == 1:
        bc[i, 1] += 0.01 * t

vn = arap.solve(bc, v)
mp.plot(vn, f, c)

Various Examples (Eigendecomposition)

from scipy.sparse.linalg import eigsh

v, f, _ = igl.read_off("data/beetle.off")
l = -igl.cotmatrix(v, f)
d, u = eigsh(l, 10, sigma=0, which="LM")

mp.plot(v, f, u[:, 5])

Various Examples (Exact Geodesics)

v, f = igl.read_triangle_mesh("data/bunny.obj")

# Select a vertex as origin
vs = np.array([0])

# All vertices are the targets
vt = np.arange(v.shape[0])

d = igl.exact_geodesic(v, f, vs, vt)

# Visualize with periodic function
c = np.abs(np.sin((d / 0.03 * np.pi)))
p = mp.plot(v, f, c)
p.add_points(v[vs], shading={"point_size": 0.05})

Various Examples (Ambient Occlusion)

v, f = igl.read_triangle_mesh("data/fertility.off")

n = igl.per_vertex_normals(v, f)

# Compute ambient occlusion factor using embree
ao = igl.ambient_occlusion(v, f, v, n, 50)
ao = 1.0 - ao

mp.plot(v, f, ao, shading={"colormap": "gist_gray"})

Various Examples (Subdivision Surfaces)

ov, of = igl.read_triangle_mesh("data/decimated-knight.off")
uv, uf = igl.upsample(ov, of)
lv, lf = igl.loop(ov, of)

mp.plot(ov, of, shading={"wireframe": True})

mp.plot(uv, uf, shading={"wireframe": True})

mp.plot(lv, lf, shading={"wireframe": True})